What Is a Merkle Tree in Blockchain and How Does It Work?

Technology enthusiasts interested in finding out more about the revolutionary technology that blockchain is, must have often wondered : “what is a Merkle Tree in blockchain and how does it work?” Let’s try to find out the answer to these questions one by one and attempt to gather an insight into this interesting element of blockchain technology.

What Is a Merkle Tree in Blockchain?

Also known as a hash tree, a Merkle Tree is an imperative unit of blockchain technology. It refers to a structure which makes it possible to efficiently verify all the contents in a large set of information. This aspect of the technology is crucial for making sure the verification process can be carried out in a secure manner. Both Ethereum and Bitcoin blockchain networks make use of it to validate whether a large body of information is accurate and consistent or not.

A Merkle Tree is created in such a way that blocks updated with information can easily be transferred from one peer to another, without having been modified or corrupted in any manner. Most of the Merkle Trees have a dual child node system situated under each node that exists on the network. However, more than just two child modes can possibly exist within a Merkle Tree. The Merkle Tree allows for the accurate verification of all data contained in a large set without having to scrutinize every single transaction.

How does a Merkle Tree Work in a Blockchain Network?

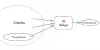
A Merkle Tree generates a common digital fingerprint to represent a large set of transactions at one go. By using this fingerprint, a user can easily make sure whether or not the block includes a particular transaction. In order to create a Merkle Tree, one has to continuously and repeatedly hash node pairs till the process leaves behind just one hash, which serves as the root for this tree structure. This is known as the Merkle Root. These hashes are created from the individual transaction hashes moving bottom up.

This tree is made up of leaves that are basically nodes representing the hashes of the transactional information within the block. There are non-leaf nodes as well, which basically serve as the hashes of the hashes before it. Since this is a binary technology, the leaf nodes must be present in an even number. If there are four transactions within a block namely W,X,Y and Z. Every transaction here will be hashed, and the hash contained in a leaf code, to subsequently give rise to hashes W,X, Y and Z. Now, these leaf nodes will then be summarised in consecutive pairings, forming hashes WX and YZ. These will have to be hashed together again in order to generate the Merkle Root. Similarly, this process can be implemented on much larger sets of information, hashing consecutive blocks till the last node is reached. Normally, the cryptographic function that is commonly used for this is SHA-2 although other functions are as good when it comes to hashing in a Merkle Tree.

What does a Merkle Tree Do In Blockchain Technology?

The Merkle Tree creates one block header using a summary of all the information contained in the transactions of a block. Even if one tiny detail from any of these transactions changes, the Merkle Root must be changed as well. The Merkle Tree technology helps to confirm whether or not a particular transaction is present in a set. Unlike a hash list, a Merkle Tree can be broken down into single branches and downloaded. If the original version of the data gets corrupted, then just the copy of that can be downloaded and saved. Thus, Merkle Tree enhances the security of blockchain databases.